Due to their relevance in pharmaceuticals, organic semiconductor materials, and many other applications, the interest in molecular crystals has grown in the past decade. Electronic structure methods are a mandatory tool to model those systems accurately on a quantum mechanical level. While formally exact solutions can be formulated, real live applications have to be sufficiently fast in order to provide computed results in a reasonable time frame.
Thus, my research concentrates on the development and application of fast electronic structure methods, with particular focus on organic crystals and their polymorph prediction. The following sections highlight some of my recent research in the areas.
London dispersion interactions
London dispersion interactions are also known as attractive part of the van der Waals forces and are omnipresent in all electronic systems. They arise as zero-point vibration of coupled charge fluctuations and are a purely quantum mechanically interaction without classical analog. The dispersion interaction can be viewed as the long-range limit of the correlation energy. For this, an exact expression can be formulated from the adiabatic fluctuation dissipation theorem
The dynamical response function involved is way to complicated to be computed for our systems of interest with about 10³ interacting electrons. Thus, a typical approach is the usage of an effective mean field theory like density funcational theory (DFT) or Hartree-Fock (HF) combined with a dispersion correction that approximates the above expression.
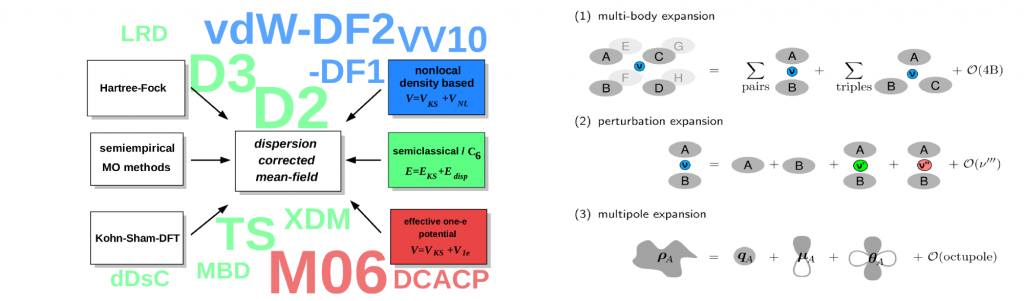
Typically, the response function is locally partitioned into fragments (usually atoms) and subsequently the interaction is described perturbatively while the perturbing field is expanded into multipoles. Modern state-of-the-art dispersion corrections differ in (1) the order in the many-body perturbation theory, (2) the truncation of the mulipole expansion, (3) the partitioning in which the atom-in-molecules (or solid) dispersion coefficients are obtained, and (4) the shape of the damping function that connects the correction scheme with the underlying mean field model.
My work mostly involves the semiclassical D3 dispersion correction mainly developed by Stefan Grimme. This model exhibits a number of appealing features. First, it has a very low computational complexity and can be combined with intrinsically extremely fast electronic structure methods. This is due to its dependency on the molecular geometry only without density based information that requires integration of properties on a real space grid. Second, it can be applied for practically the whole periodic table and provides the correct long-range limit for all finite gap systems. Finally, the accuracy is excellent and similar to more complex density based procedures. For instance mass densities of organic crystals can be computed with small residuum error of about 1-3% and electronic lattice energies are close to or within the chemical accuracy of 1 kcal/mol. I have compiled a new benchmark set of ice polymorphs, which mainly confirms the accuracies though the focus is on electrostatic and induction interactions.
For more information, see for example
- S. Grimme, A. Hansen, J. G. Brandenburg, and C. Bannwarth, “Dispersion-corrected mean-field electronic structure methods,” Chem. Rev., vol. 116, pp. 5105-5154, 2016. doi:10.1021/acs.chemrev.5b00533
[BibTeX] [Abstract] [Download PDF]
Mean-field electronic structure methods like Hartree−Fock, semilocal density functional approximations, or semiempirical molecular orbital (MO) theories do not account for long-range electron correlations (London dispersion interaction). Inclusion of these effects is mandatory for realistic calculations on large or condensed chemical systems and for various intramolecular phenomena (thermochemistry). This Review describes the recent developments (including some historical aspects) of dispersion corrections with an emphasis on methods that can be employed routinely with reasonable accuracy in large-scale applications. The most prominent correction schemes were classified into three groups: (i) nonlocal, density-based functionals, (ii) semiclassical C6-based, and (iii) one-electron effective potentials. The properties as well as pros and cons of these methods are critically discussed, and typical examples and benchmarks on molecular complexes and crystals are provided. Although there are some areas for further improvement (robustness, many-body and short-range effects), the situation regarding the overall accuracy is clear. Various approaches yield long-range dispersion energy with a typical relative error of 5\%. For many chemical problems, this accuracy is higher compared to the underlying mean-field method (i.e., a typical semilocal (hybrid) functional like B3LYP).
@article {brandenburg_ref18, author = {S. Grimme and A. Hansen and J. G. Brandenburg and C. Bannwarth}, title = {Dispersion-corrected mean-field electronic structure methods}, journal = {{Chem. Rev.}}, volume = {116}, pages = {5105-5154}, year = {2016}, doi = {10.1021/acs.chemrev.5b00533}, url = {../wp-content/papercite-data/pdf/brandenburg_ref18.pdf}, abstract = {Mean-field electronic structure methods like Hartree−Fock, semilocal density functional approximations, or semiempirical molecular orbital (MO) theories do not account for long-range electron correlations (London dispersion interaction). Inclusion of these effects is mandatory for realistic calculations on large or condensed chemical systems and for various intramolecular phenomena (thermochemistry). This Review describes the recent developments (including some historical aspects) of dispersion corrections with an emphasis on methods that can be employed routinely with reasonable accuracy in large-scale applications. The most prominent correction schemes were classified into three groups: (i) nonlocal, density-based functionals, (ii) semiclassical C6-based, and (iii) one-electron effective potentials. The properties as well as pros and cons of these methods are critically discussed, and typical examples and benchmarks on molecular complexes and crystals are provided. Although there are some areas for further improvement (robustness, many-body and short-range effects), the situation regarding the overall accuracy is clear. Various approaches yield long-range dispersion energy with a typical relative error of 5\%. For many chemical problems, this accuracy is higher compared to the underlying mean-field method (i.e., a typical semilocal (hybrid) functional like B3LYP).} }
- J. G. Brandenburg, T. Maas, and S. Grimme, “Benchmarking dft and semiempirical methods on structures and lattice energies for ten ice polymorphs,” J. Chem. Phys., vol. 142, p. 124104, 2015. doi:10.1063/1.4916070
[BibTeX] [Abstract] [Download PDF]
Water in different phases under various external conditions is very important in bio-chemical systems and for material science at surfaces. Density functional theory methods and approximations thereof have to be tested system specifically to benchmark their accuracy regarding computed structures and interaction energies. In this study, we present and test a set of ten ice polymorphs in comparison to experimental data with mass densities ranging from 0.9 to 1.5 g/cm$^3$ and including explicit corrections for zero-point vibrational and thermal effects. London dispersion inclusive density functionals at the generalized gradient approximation (GGA), meta-GGA, and hybrid level as well as alternative low-cost molecular orbital methods are considered. The widely used functional of Perdew, Burke and Ernzerhof (PBE) systematically overbinds and overall provides inconsistent results. All other tested methods yield reasonable to very good accuracy. BLYP-D3$^{atm}$ gives excellent results with mean absolute errors for the lattice energy below 1 kcal/mol (7\% relative deviation). The corresponding optimized structures are very accurate with mean absolute relative deviations (MARDs) from the reference unit cell volume below 1\%. The impact of Axilrod-Teller-Muto (atm) type three-body dispersion and of non-local Fock exchange is small but on average their inclusion improves the results. While the density functional tight-binding model DFTB3-D3 performs well for low density phases, it does not yield good high density structures. As low-cost alternative for structure related problems, we recommend the recently introduced minimal basis Hartree-Fock method HF-3c with a MARD of about 3\%.
@article{brandenburg_ref12, author = {J. G. Brandenburg and T. Maas and S. Grimme}, title = {Benchmarking DFT and semiempirical methods on structures and lattice energies for ten ice polymorphs}, journal = {{J. Chem. Phys.}}, year = {2015}, volume = {142}, pages = {124104}, doi = {10.1063/1.4916070}, url = {../wp-content/papercite-data/pdf/brandenburg_ref12.pdf}, abstract = {Water in different phases under various external conditions is very important in bio-chemical systems and for material science at surfaces. Density functional theory methods and approximations thereof have to be tested system specifically to benchmark their accuracy regarding computed structures and interaction energies. In this study, we present and test a set of ten ice polymorphs in comparison to experimental data with mass densities ranging from 0.9 to 1.5 g/cm$^3$ and including explicit corrections for zero-point vibrational and thermal effects. London dispersion inclusive density functionals at the generalized gradient approximation (GGA), meta-GGA, and hybrid level as well as alternative low-cost molecular orbital methods are considered. The widely used functional of Perdew, Burke and Ernzerhof (PBE) systematically overbinds and overall provides inconsistent results. All other tested methods yield reasonable to very good accuracy. BLYP-D3$^{atm}$ gives excellent results with mean absolute errors for the lattice energy below 1 kcal/mol (7\% relative deviation). The corresponding optimized structures are very accurate with mean absolute relative deviations (MARDs) from the reference unit cell volume below 1\%. The impact of Axilrod-Teller-Muto (atm) type three-body dispersion and of non-local Fock exchange is small but on average their inclusion improves the results. While the density functional tight-binding model DFTB3-D3 performs well for low density phases, it does not yield good high density structures. As low-cost alternative for structure related problems, we recommend the recently introduced minimal basis Hartree-Fock method HF-3c with a MARD of about 3\%.} }
- R. J. Maurer, C. Freysoldt, A. M. Reilly, J. G. Brandenburg, O. T. Hofmann, T. Bjöorkman, S. Lebègue, and A. Tkatchenko, “Advances in density-functional calculations for materials modeling,” Annu. Rev. Mater. Res., vol. 49, p. 3.1-3.30, 2019. doi:10.1146/annurev-matsci-070218-010143
[BibTeX] [Abstract]
During the past two decades, density-functional (DF) theory has evolved from niche applications to simple solid-state materials, becoming a workhorse method for studying a wide range of phenomena in a variety of system classes throughout physics, chemistry, biology, and materials science. Here, we review the recent advances in DF calculations for materials modeling, giving a classification of modern DF-based methods when viewed from the materials modeling perspective. While the progress has been very substantial, many challenges remain on the way to achieve consensus on a set of universally applicable DF-based methods for materials modeling. Hence, we focus on recent successes and remaining challenges in DF calculations for modeling hard solids, molecular and biological matter, low-dimensional materials, and hybrid organic-inorganic materials.
@Article{brandenburg_ref43, author ={R. J. Maurer and C. Freysoldt and A. M. Reilly and J. G. Brandenburg and O. T. Hofmann and T. Bj\"{o}orkman and S. Leb\`{e}gue and A. Tkatchenko}, title ={Advances in Density-Functional Calculations for Materials Modeling}, journal ={{Annu. Rev. Mater. Res.}}, year ={2019}, volume = {49}, pages ={3.1-3.30}, doi = {10.1146/annurev-matsci-070218-010143}, abstract ={During the past two decades, density-functional (DF) theory has evolved from niche applications to simple solid-state materials, becoming a workhorse method for studying a wide range of phenomena in a variety of system classes throughout physics, chemistry, biology, and materials science. Here, we review the recent advances in DF calculations for materials modeling, giving a classification of modern DF-based methods when viewed from the materials modeling perspective. While the progress has been very substantial, many challenges remain on the way to achieve consensus on a set of universally applicable DF-based methods for materials modeling. Hence, we focus on recent successes and remaining challenges in DF calculations for modeling hard solids, molecular and biological matter, low-dimensional materials, and hybrid organic-inorganic materials.} }
Cost-efficient methods for organic crystals
Dispersion-corrected density functional theory (DFT-D) is in principle applicable to many interesting targets. However, the computational demands, for example, to sample a huge number of polymorphs, are still too high. I have (co-)developed a number of cost-efficient schemes to model molecular complexes and organic crystals in particular.
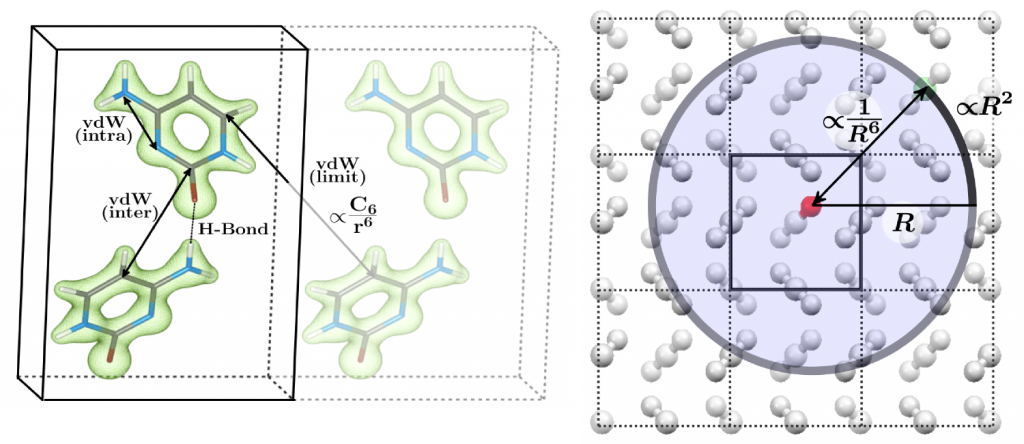
These range from semiempirical tight-binding methods (DFTB3-D3) to density functional based methods (PBEh-3c, HSE-3c, B97-3c). Due to their partially empirical character, a rigorous benchmarking is mandatory. This involves energetic and geometric properties of both gas phase and solid phase systems. Some typical benchmark results are shown below with the dispersion corrected meta generalized gradient approximated (GGA) functional TPSS-D3 in converged projector augmented plane wave (PAW) basis sets, the popular uncorrected B3LYP hybrid functional in a small single particle basis set of double-zeta quality, and the semiempirical density functional tight binding DFTB3. The importance of a proper dispersion correction is apparent and my recommended method TPSS-D3 and the low-cost alternative DFTB3-D3 perform excellently.
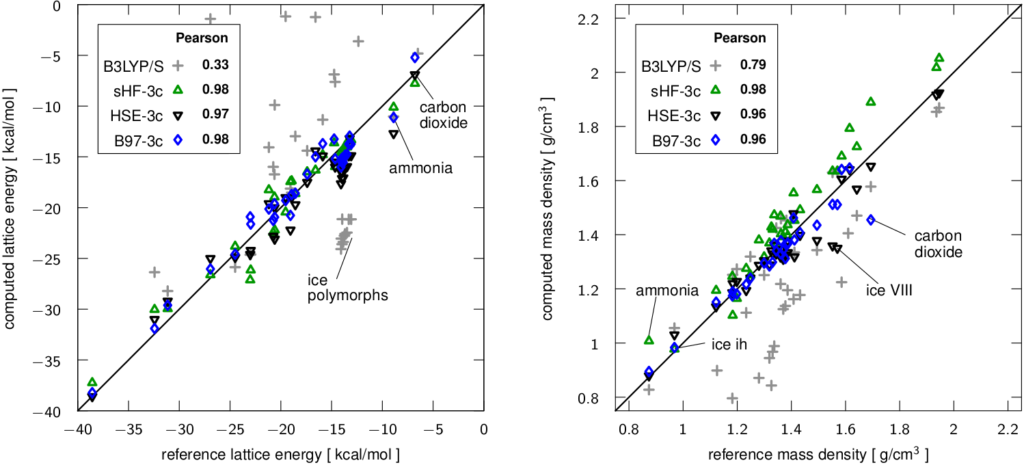
For more information, see for example
- J. G. Brandenburg and S. Grimme, “Accurate modeling of organic molecular crystals by dispersion-corrected density functional tight-binding (DFTB),” J. Phys. Chem. Lett., vol. 5, p. 1785–1789, 2014. doi:10.1021/jz500755u
[BibTeX] [Abstract] [Download PDF]
The ambitious goal of organic crystal structure prediction challenges theoretical methods regarding their accuracy and efficiency. Dispersion-corrected density functional theory (DFT-D) in principle is applicable, but the computational demands, for example, to compute a huge number of polymorphs, are too high. Here, we demonstrate that this task can be carried out by a dispersion-corrected density functional tight binding (DFTB) method. The semiempirical Hamiltonian with the D3 correction can accurately and efficiently model both solid- and gas-phase inter- and intramolecular interactions at a speed up of 2 orders of magnitude compared to DFT-D. The mean absolute deviations for interaction (lattice) energies for various databases are typically 2-3 kcal/mol (10-20\%), that is, only about two times larger than those for DFT-D. For zero-point phonon energies, small deviations of $<$0.5 kcal/mol compared to DFT-D are obtained.
@article{brandenburg_ref07, author = {J. G. Brandenburg and S. Grimme}, title = {Accurate modeling of organic molecular crystals by dispersion-corrected density functional tight-binding {(DFTB)}}, journal = {{J. Phys. Chem. Lett.}}, year = {2014}, volume = {5}, pages = {1785--1789}, doi = {10.1021/jz500755u}, url = {../wp-content/papercite-data/pdf/brandenburg_ref07.pdf}, abstract = {The ambitious goal of organic crystal structure prediction challenges theoretical methods regarding their accuracy and efficiency. Dispersion-corrected density functional theory (DFT-D) in principle is applicable, but the computational demands, for example, to compute a huge number of polymorphs, are too high. Here, we demonstrate that this task can be carried out by a dispersion-corrected density functional tight binding (DFTB) method. The semiempirical Hamiltonian with the D3 correction can accurately and efficiently model both solid- and gas-phase inter- and intramolecular interactions at a speed up of 2 orders of magnitude compared to DFT-D. The mean absolute deviations for interaction (lattice) energies for various databases are typically 2-3 kcal/mol (10-20\%), that is, only about two times larger than those for DFT-D. For zero-point phonon energies, small deviations of $<$0.5 kcal/mol compared to DFT-D are obtained. } }
- S. Grimme, J. G. Brandenburg, C. Bannwarth, and A. Hansen, "Consistent structures and interactions by density functional theory with small atomic orbital basis sets," J. Chem. Phys., vol. 143, p. 54107, 2015. doi:10.1063/1.4927476
[BibTeX] [Abstract] [Download PDF]
A density functional theory (DFT) based composite electronic structure approach is proposed to efficiently compute structures and interaction energies in large chemical systems. It is based on the well-known and numerically robust Perdew-Burke-Ernzerhoff (PBE) generalized-gradient-approximation in a modified global hybrid functional with a relatively large amount of non-local Fock-exchange. The orbitals are expanded in Ahlrichs-type valence-double zeta atomic orbital (AO) Gaussian basis sets, which are available for many elements. In order to correct for the basis set superposition error (BSSE) and to account for the important long-range London dispersion effects, our well-established atom-pairwise potentials are used. In the design of the new method, particular attention has been paid to an accurate description of structural parameters in various covalent and non-covalent bonding situations as well as in periodic systems. Together with the recently proposed three-fold corrected (3c) Hartree-Fock method, the new composite scheme (termed PBEh-3c) represents the next member in a hierarchy of “low-cost” electronic structure approaches. They are mainly free of BSSE and account for most interactions in a physically sound and asymptotically correct manner. PBEh-3c yields good results for thermochemical properties in the huge GMTKN30 energy database. Furthermore, the method shows excellent performance for non-covalent interaction energies in small and large complexes. For evaluating its performance on equilibrium structures, a new compilation of standard test sets is suggested. These consist of small (light) molecules, partially flexible, medium-sized organic molecules, molecules comprising heavy main group elements, larger systems with long bonds, 3d-transition metal systems, non-covalently bound complexes (S22 and S66×8 sets), and peptide conformations. For these sets, overall deviations from accurate reference data are smaller than for various other tested DFT methods and reach that of triple-zeta AO basis set second-order perturbation theory (MP2/TZ) level at a tiny fraction of computational effort. Periodic calculations conducted for molecular crystals to test structures (including cell volumes) and sublimation enthalpies indicate very good accuracy competitive to computationally more involved plane-wave based calculations. PBEh-3c can be applied routinely to several hundreds of atoms on a single processor and it is suggested as a robust “high-speed” computational tool in theoretical chemistry and physics.
@article{brandenburg_ref14, author = {S. Grimme and J. G. Brandenburg and C. Bannwarth and A. Hansen}, title = {Consistent structures and interactions by density functional theory with small atomic orbital basis sets}, journal = {{J. Chem. Phys.}}, year = {2015}, volume = {143}, pages = {054107}, doi = {10.1063/1.4927476}, url = {../wp-content/papercite-data/pdf/brandenburg_ref14.pdf}, abstract = {A density functional theory (DFT) based composite electronic structure approach is proposed to efficiently compute structures and interaction energies in large chemical systems. It is based on the well-known and numerically robust Perdew-Burke-Ernzerhoff (PBE) generalized-gradient-approximation in a modified global hybrid functional with a relatively large amount of non-local Fock-exchange. The orbitals are expanded in Ahlrichs-type valence-double zeta atomic orbital (AO) Gaussian basis sets, which are available for many elements. In order to correct for the basis set superposition error (BSSE) and to account for the important long-range London dispersion effects, our well-established atom-pairwise potentials are used. In the design of the new method, particular attention has been paid to an accurate description of structural parameters in various covalent and non-covalent bonding situations as well as in periodic systems. Together with the recently proposed three-fold corrected (3c) Hartree-Fock method, the new composite scheme (termed PBEh-3c) represents the next member in a hierarchy of “low-cost” electronic structure approaches. They are mainly free of BSSE and account for most interactions in a physically sound and asymptotically correct manner. PBEh-3c yields good results for thermochemical properties in the huge GMTKN30 energy database. Furthermore, the method shows excellent performance for non-covalent interaction energies in small and large complexes. For evaluating its performance on equilibrium structures, a new compilation of standard test sets is suggested. These consist of small (light) molecules, partially flexible, medium-sized organic molecules, molecules comprising heavy main group elements, larger systems with long bonds, 3d-transition metal systems, non-covalently bound complexes (S22 and S66×8 sets), and peptide conformations. For these sets, overall deviations from accurate reference data are smaller than for various other tested DFT methods and reach that of triple-zeta AO basis set second-order perturbation theory (MP2/TZ) level at a tiny fraction of computational effort. Periodic calculations conducted for molecular crystals to test structures (including cell volumes) and sublimation enthalpies indicate very good accuracy competitive to computationally more involved plane-wave based calculations. PBEh-3c can be applied routinely to several hundreds of atoms on a single processor and it is suggested as a robust “high-speed” computational tool in theoretical chemistry and physics.} }
- J. G. Brandenburg, C. Bannwarth, A. Hansen, and S. Grimme, "B97-3c: a revised low-cost variant of the b97-d density functional method," J. Chem. Phys., vol. 148, p. 64104, 2018. doi:10.1063/1.5012601
[BibTeX] [Abstract] [Download PDF]
A revised version of the well-established B97-D density functional approximation with general applicability for chemical properties of large systems is proposed. Like B97-D, it is based on Becke's power-series ansatz from 1997 and is explicitly parametrized by including the standard D3 semi-classical dispersion correction. The orbitals are expanded in a modified valence triple-zeta Gaussian basis set, which is available for all elements up to Rn. Remaining basis set errors are mostly absorbed in the modified B97 parametrization, while an established atom-pairwise short-range potential is applied to correct for the systematically too long bonds of main group elements which are typical for most semi-local density functionals. The new composite scheme (termed B97-3c) completes the hierarchy of "low-cost" electronic structure methods, which are all mainly free of basis set superposition error (BSSE) and account for most interactions in a physically sound and asymptotically correct manner. B97-3c yields excellent molecular and condensed phase geometries, similar to most hybrid functionals evaluated in a larger basis set expansion. Results on the comprehensive GMTKN55 energy database demonstrate its good performance for main group thermochemistry, kinetics, and non-covalent interactions, when compared to functionals of the same class. This also transfers to metal-organic reactions, which is a major area of applicability for semi-local functionals. B97-3c can be routinely applied to hundreds of atoms on a single processor and we suggest it as a robust computational tool, in particular, for more strongly correlated systems where our previously published "3c" schemes might be problematic.
@article{brandenburg_ref34, author = {J. G. Brandenburg and C. Bannwarth and A. Hansen and S. Grimme}, title = {B97-3c: A revised low-cost variant of the B97-D density functional method}, journal = {{J. Chem. Phys.}}, volume = {148}, pages = {064104}, year = {2018}, doi = {10.1063/1.5012601}, url = {../wp-content/papercite-data/pdf/brandenburg_ref34.pdf}, abstract={A revised version of the well-established B97-D density functional approximation with general applicability for chemical properties of large systems is proposed. Like B97-D, it is based on Becke's power-series ansatz from 1997 and is explicitly parametrized by including the standard D3 semi-classical dispersion correction. The orbitals are expanded in a modified valence triple-zeta Gaussian basis set, which is available for all elements up to Rn. Remaining basis set errors are mostly absorbed in the modified B97 parametrization, while an established atom-pairwise short-range potential is applied to correct for the systematically too long bonds of main group elements which are typical for most semi-local density functionals. The new composite scheme (termed B97-3c) completes the hierarchy of "low-cost" electronic structure methods, which are all mainly free of basis set superposition error (BSSE) and account for most interactions in a physically sound and asymptotically correct manner. B97-3c yields excellent molecular and condensed phase geometries, similar to most hybrid functionals evaluated in a larger basis set expansion. Results on the comprehensive GMTKN55 energy database demonstrate its good performance for main group thermochemistry, kinetics, and non-covalent interactions, when compared to functionals of the same class. This also transfers to metal-organic reactions, which is a major area of applicability for semi-local functionals. B97-3c can be routinely applied to hundreds of atoms on a single processor and we suggest it as a robust computational tool, in particular, for more strongly correlated systems where our previously published "3c" schemes might be problematic. } }
- E. Caldeweyher and J. G. Brandenburg, "Simplified dft methods for consistent structures and energies of large systems," J. Phys.: Condens. Matter, vol. 30, p. 213001, 2018. doi:10.1088/1361-648X/aabcfb
[BibTeX] [Abstract]
Kohn-Sham density functional theory (DFT) is routinely used for the fast electronic structure computation of large systems and will most likely continue to be the method of choice for the generation of reliable geometries in the foreseeable future. Here, we present a hierarchy of simplified DFT methods designed for consistent structures and non-covalent interactions of large systems with particular focus on molecular crystals. The covered methods are a minimal basis set Hartree-Fock (HF-3c), a small basis set screened exchange hybrid functional (HSE-3c), and a generalized gradient approximated functional evaluated in a medium sized basis set (B97-3c), all augmented with semi-classical correction potentials. We give an overview on the methods design, a comprehensive evaluation on established benchmark sets for geometries and lattice energies of molecular crystals, and highlight some realistic applications on large organic crystals with several hundreds of atoms in the primitive unit cell.
@Article{brandenburg_ref36, author ={E. Caldeweyher and J. G. Brandenburg}, title ={Simplified DFT methods for consistent structures and energies of large systems}, journal ={{J. Phys.: Condens. Matter}}, year ={2018}, volume = {30}, pages = {213001}, doi ={10.1088/1361-648X/aabcfb}, abstract ={Kohn-Sham density functional theory (DFT) is routinely used for the fast electronic structure computation of large systems and will most likely continue to be the method of choice for the generation of reliable geometries in the foreseeable future. Here, we present a hierarchy of simplified DFT methods designed for consistent structures and non-covalent interactions of large systems with particular focus on molecular crystals. The covered methods are a minimal basis set Hartree-Fock (HF-3c), a small basis set screened exchange hybrid functional (HSE-3c), and a generalized gradient approximated functional evaluated in a medium sized basis set (B97-3c), all augmented with semi-classical correction potentials. We give an overview on the methods design, a comprehensive evaluation on established benchmark sets for geometries and lattice energies of molecular crystals, and highlight some realistic applications on large organic crystals with several hundreds of atoms in the primitive unit cell.} }
Organic crystal structure prediction
The polymorphism of molecular crystals is important in various areas of chemistry and physics with possible applications for pharmaceutical compounds, pigments, explosives, and metal-organic framework materials. Many well known generic drugs such as aspirin and paracetamol have multiple polymorphs. Because the polymorph might have different properties (e.g. solubility) pharmaceutical companies have to screen the polymorph landscape. Simulation techniques can help and guide experimentalists by supplying them with computed crystal energy landscapes.
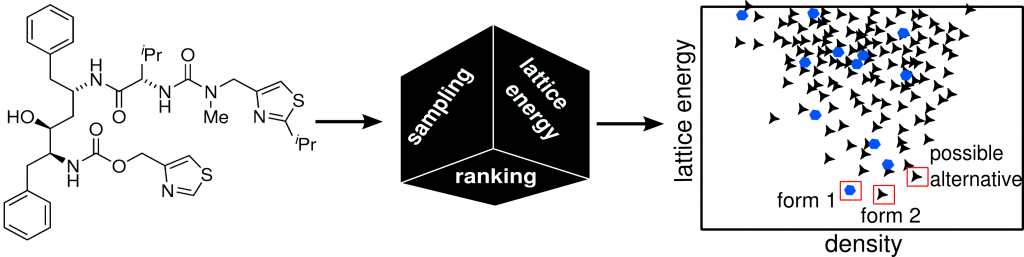
The most stable crystal structures shall be predicted from the knowledge of their molecular composition. The computed energy landscape can then be used to identify the measured structures and to suggest plausible alternative polymorphs.
Last year, I participated in the 6th blind challenge for organic crystal structure prediction organized by the Cambridge structural database. For more information, have a look at the CSP homepage and the press release concerning the latest predictions with "Best Results Ever!" As the target molecules are approaching realistic real live applications (hydrated salt, co-crystal, high flexibility), the outcome is indeed promising and I am happy to contribute to some extend.
Using Sally (L) Price generated polymorphs (1000 per target molecule), a refinement using some of the above mentioned methods (DFTB3-D3, HF-3c, TPSS-D3) is conducted. While a few polymorphs have been lost during the refinement stages, the final TPSS-D3 energy ranking is excellent and among the best ones provided so far for these targets.
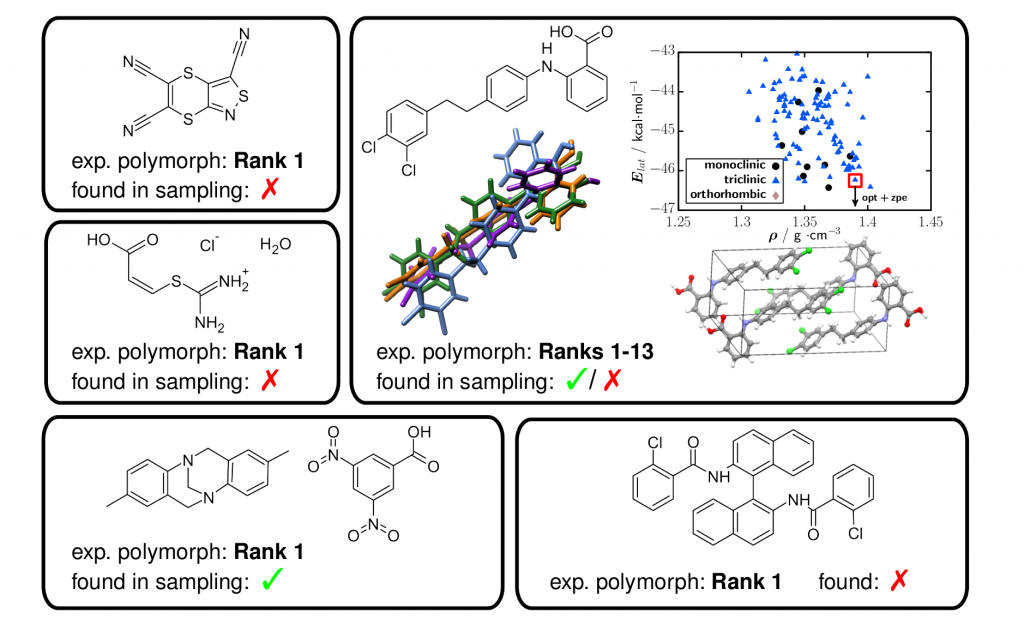
For more information, see for example:
- A. M. Reilly, R. I. Cooper, C. S. Adjiman, S. Bhattacharya, D. A. Boese, J. G. Brandenburg, P. J. Bygrave, R. Bylsma, J. E. Campbell, R. Car, D. H. Case, R. Chadha, J. C. Cole, K. Cosburn, H. M. Cuppen, F. Curtis, G. M. Day, R. A. {DiStasio Jr}, A. Dzyabchenko, B. P. van Eijck, D. M. Elking, J. A. van den Ende, J. C. Facelli, M. B. Ferraro, L. Fusti-Molnar, C. Gatsiou, T. S. Gee, R. de Gelder, L. M. Ghiringhelli, H. Goto, S. Grimme, R. Guo, D. W. M. Hofmann, J. Hoja, R. K. Hylton, L. Iuzzolino, W. Jankiewicz, D. T. de Jong, J. Kendrick, N. J. J. de Klerk, H. Ko, L. N. Kuleshova, X. Li, S. Lohani, F. J. J. Leusen, A. M. Lund, J. Lv, Y. Ma, N. Marom, A. E. Masunov, P. McCabe, D. P. McMahon, H. Meekes, M. P. Metz, A. J. Misquitta, S. Mohamed, B. Monserrat, R. J. Needs, M. A. Neumann, J. Nyman, S. Obata, H. Oberhofer, A. R. Oganov, A. M. Orendt, G. I. Pagola, C. C. Pantelides, C. J. Pickard, R. Podeszwa, L. S. Price, S. L. Price, A. Pulido, M. G. Read, K. Reuter, E. Schneider, C. Schober, G. P. Shields, P. Singh, I. J. Sugden, K. Szalewicz, C. R. Taylor, A. Tkatchenko, M. E. Tuckerman, F. Vacarro, M. Vasileiadis, A. Vázquez-Mayagoitia, L. Vogt, Y. Wang, R. E. Watson, G. A. de Wijs, J. Yang, Q. Zhu, and C. R. Groom, "Report on the sixth blind test of organic crystal-structure prediction methods," Acta Cryst. B, vol. 72, pp. 439-459, 2016. doi:10.1107/S2052520616007447
[BibTeX] [Abstract] [Download PDF]
The sixth blind test of organic crystal-structure prediction (CSP) methods has been held, with five target systems: a small nearly rigid molecule, a polymorphic former drug candidate, a chloride salt hydrate, a co-crystal, and a bulky flexible molecule. This blind test has seen substantial growth in the number of submissions, with the broad range of prediction methods giving a unique insight into the state of the art in the field. Significant progress has been seen in treating flexible molecules, usage of hierarchical approaches to ranking structures, the application of density-functional approximations, and the establishment of new workflows and “best practices” forperforming CSP calculations. All of the targets, apart from a single potentially disordered Z = 2 polymorph of the drug candidate, were predicted by at least one submission. Despite many remaining challenges, it is clear that CSP methods are becoming more applicable to a wider range of real systems, including salts, hydrates and larger flexible molecules. The results also highlight the potential for CSP calculations to complement and augment experimental studies of organic solid forms.
@article {brandenburg_ref19, author = {Reilly, Anthony M. and Cooper, Richard I. and Adjiman, Claire S. and Bhattacharya, Saswata and Boese, A. Daniel and Brandenburg, Jan Gerit and Bygrave, Peter J. and Bylsma, Rita and Campbell, Josh E. and Car, Roberto and Case, David H. and Chadha, Renu and Cole, Jason C. and Cosburn, Katherine and Cuppen, Herma M. and Curtis, Farren and Day, Graeme M. and {DiStasio Jr}, Robert A. and Dzyabchenko, Alexander and van Eijck, Bouke P. and Elking, Dennis M. and van den Ende, Joost A. and Facelli, Julio C. and Ferraro, Marta B. and Fusti-Molnar, Laszlo and Gatsiou, Christina-Anna and Gee, Thomas S. and de Gelder, R{\'e}ne and Ghiringhelli, Luca M. and Goto, Hitoshi and Grimme, Stefan and Guo, Rui and Hofmann, Detlef W.M. and Hoja, Johannes and Hylton, Rebecca K. and Iuzzolino, Luca and Jankiewicz, Wojciech and de Jong, Dani{\"e}l T. and Kendrick, John and de Klerk, Niek J.J. and Ko, Hsin-Yu and Kuleshova, Liudmila N. and Li, Xiayue and Lohani, Sanjaya and Leusen, Frank J.J. and Lund, Albert M. and Lv, Jian and Ma, Yanming and Marom, Noa and Masunov, Art{\"e}m E. and McCabe, Patrick and McMahon, David P. and Meekes, Hugo and Metz, Michael P. and Misquitta, Alston J. and Mohamed, Sharmarke and Monserrat, Bartomeu and Needs, Richard J. and Neumann, Marcus A. and Nyman, Jonas and Obata, Shigeaki and Oberhofer, Harald and Oganov, Artem R. and Orendt, Anita M. and Pagola, Gabriel I. and Pantelides, Constantinos C. and Pickard, Chris J. and Podeszwa, Rafa\l{} and Price, Louise S. and Price, Sarah L. and Pulido, Angeles and Read, Murray G. and Reuter, Karsten and Schneider, Elia and Schober, Christoph and Shields, Gregory P. and Singh, Pawanpreet and Sugden, Isaac J. and Szalewicz, Krzysztof and Taylor, Christopher R. and Tkatchenko, Alexandre and Tuckerman, Mark E. and Vacarro, Francesca and Vasileiadis, Manolis and V{\'a}zquez-Mayagoitia, Alvaro and Vogt, Leslie and Wang, Yanchao and Watson, Rona E. and de Wijs, Gilles A. and Yang, Jack and Zhu, Qiang and Groom, Colin R.}, title = {Report on the sixth blind test of organic crystal-structure prediction methods}, journal = {{Acta Cryst. B}}, volume = {72}, pages = {439-459}, year = {2016}, doi = {10.1107/S2052520616007447}, url = {../wp-content/papercite-data/pdf/brandenburg_ref19.pdf}, abstract = {The sixth blind test of organic crystal-structure prediction (CSP) methods has been held, with five target systems: a small nearly rigid molecule, a polymorphic former drug candidate, a chloride salt hydrate, a co-crystal, and a bulky flexible molecule. This blind test has seen substantial growth in the number of submissions, with the broad range of prediction methods giving a unique insight into the state of the art in the field. Significant progress has been seen in treating flexible molecules, usage of hierarchical approaches to ranking structures, the application of density-functional approximations, and the establishment of new workflows and “best practices” forperforming CSP calculations. All of the targets, apart from a single potentially disordered Z = 2 polymorph of the drug candidate, were predicted by at least one submission. Despite many remaining challenges, it is clear that CSP methods are becoming more applicable to a wider range of real systems, including salts, hydrates and larger flexible molecules. The results also highlight the potential for CSP calculations to complement and augment experimental studies of organic solid forms.} }
- S. L. Price and J. G. Brandenburg, Molecular crystal structure prediction, Melbourne, Australia: Elsevier, 2017, vol. Non-covalent interactions in quantum chemistry and physics, Eds. G. DiLabio, A. Otero-de-la-Roza, ISBN: 9780128098356.
[BibTeX] [Abstract] [Download PDF]
Organic crystal structure prediction methods (CSP) aim to predict the crystal structure from the molecular diagram, for use in the design of new functional organic materials. CSP can help avoid the synthesis of molecules which will not give crystals with the desired physical property. However, CSP is mostly applied to determine the risk of polymorphism for molecules, such as pharmaceuticals, to aid the design of the crystallization processes used in their manufacture. CSP can complement experimental solid form screening in helping find and characterize the polymorphs of a given molecule. Most CSP methods are based on the assumption that the observed crystal structures are the most stable, or that they lie within the small energy range for thermodynamically plausible polymorphs. Thus, the generation of possible crystal structures and their energy ranking is required during the prediction. This usually provides a severe test of the model for the relative thermal stability of the computer-generated crystals. Thus, CSP has been used as a test of models for the intermolecular forces between small molecules whose solid state properties are mostly of academic significance. Interest in the organic solid state has grown, with both an increasing desire to use computers to design materials and crystallization processes, and improved experimental characterization techniques providing evidence for the inadequacies of the idealized models currently used in simulaton. Hence, there is a significant complementarity between theory and experiment that stems from finding what range of types of crystal packing and properties may be engineered.
@book{brandenburg_ref28, title = {Molecular crystal structure prediction}, publisher = {Elsevier}, address = {Melbourne, Australia}, volume = {Non-covalent interactions in quantum chemistry and physics, Eds. G. DiLabio, A. Otero-de-la-Roza, ISBN: 9780128098356}, year = {2017}, url = {https://www.elsevier.com/books/non-covalent-interactions-in-quantum-chemistry-and-physics/otero-de-la-roza/978-0-12-809835-6}, note = {ISBN: 9780128098356}, author = {S. L. Price and J. G. Brandenburg}, abstract={Organic crystal structure prediction methods (CSP) aim to predict the crystal structure from the molecular diagram, for use in the design of new functional organic materials. CSP can help avoid the synthesis of molecules which will not give crystals with the desired physical property. However, CSP is mostly applied to determine the risk of polymorphism for molecules, such as pharmaceuticals, to aid the design of the crystallization processes used in their manufacture. CSP can complement experimental solid form screening in helping find and characterize the polymorphs of a given molecule. Most CSP methods are based on the assumption that the observed crystal structures are the most stable, or that they lie within the small energy range for thermodynamically plausible polymorphs. Thus, the generation of possible crystal structures and their energy ranking is required during the prediction. This usually provides a severe test of the model for the relative thermal stability of the computer-generated crystals. Thus, CSP has been used as a test of models for the intermolecular forces between small molecules whose solid state properties are mostly of academic significance. Interest in the organic solid state has grown, with both an increasing desire to use computers to design materials and crystallization processes, and improved experimental characterization techniques providing evidence for the inadequacies of the idealized models currently used in simulaton. Hence, there is a significant complementarity between theory and experiment that stems from finding what range of types of crystal packing and properties may be engineered.} }
- L. Iuzzolino, P. McCabe, S. L. Price, and J. G. Brandenburg, "Crystal structure prediction of flexible pharmaceutical-like molecules: density functional tight-binding as an intermediate optimization method and for free energy estimation," Faraday Discuss., vol. 211, p. 275–296, 2018. doi:10.1039/C8FD00010G
[BibTeX] [Abstract] [Download PDF]
Successful methodologies for theoretical crystal structure prediction (CSP) on flexible pharmaceutical-like organic molecules explore the lattice energy surface to find a set of plausible crystal structures. The initial search stage of CSP studies uses a relatively simple lattice energy approximation as hundreds of thousands of minima have to be considered. These generated crystal structures often have poor molecular geometries{,} as well as inaccurate lattice-energy rankings{,} and performing reasonably accurate but computationally affordable optimisations of the crystal structures generated in a search would be highly desirable. Here{,} we seek to explore whether semi-empirical quantum-mechanical methods can perform this task. We employed the dispersion-corrected tight-binding Hamiltonian (DFTB3-D3) to relax all inter and intra-molecular degrees of freedom of several thousands of generated crystal structures of five pharmaceutical-like molecules{,} saving a large amount of computational effort compared to earlier studies. The computational cost scales better with molecular size and flexibility than other CSP methods{,} suggesting it could be extended to even larger and more flexible molecules. On average{,} this optimisation improved the average reproduction of the eight experimental crystal structures (RMSD15 ) and experimental conformers (RMSD1) by 4% and 23%{,} respectively. The intermolecular interactions were then further optimised using distributed multipoles{,} derived from the molecular wave-function{,} to accurately describe the electrostatic component of the intermolecular energy. In all cases{,} the experimental crystal structures are close to the top of the lattice energy ranking. Phonon calculations on some of the lowest energy structures were also performed with DFTB3-D3 methods to calculate the vibrational component of the Helmholtz free energy{,} providing further insights into the solid-state behaviour of the target molecules. We conclude that DFTB3-D3 is a cost-effective method for optimising flexible molecules{,} bridging the gap between the approximate methods used in CSP searches for generating crystal structures and more accurate methods required in the final energy ranking.
@Article{brandenburg_ref35, author ={L. Iuzzolino and P. McCabe and S. L. Price and J. G. Brandenburg}, title ={Crystal structure prediction of flexible pharmaceutical-like molecules: Density functional tight-binding as an intermediate optimization method and for free energy estimation}, journal ={{Faraday Discuss.}}, year ={2018}, volume = {211}, pages = {275--296}, url = {../wp-content/papercite-data/pdf/brandenburg_ref35.pdf}, doi ={10.1039/C8FD00010G}, abstract ={Successful methodologies for theoretical crystal structure prediction (CSP) on flexible pharmaceutical-like organic molecules explore the lattice energy surface to find a set of plausible crystal structures. The initial search stage of CSP studies uses a relatively simple lattice energy approximation as hundreds of thousands of minima have to be considered. These generated crystal structures often have poor molecular geometries{,} as well as inaccurate lattice-energy rankings{,} and performing reasonably accurate but computationally affordable optimisations of the crystal structures generated in a search would be highly desirable. Here{,} we seek to explore whether semi-empirical quantum-mechanical methods can perform this task. We employed the dispersion-corrected tight-binding Hamiltonian (DFTB3-D3) to relax all inter and intra-molecular degrees of freedom of several thousands of generated crystal structures of five pharmaceutical-like molecules{,} saving a large amount of computational effort compared to earlier studies. The computational cost scales better with molecular size and flexibility than other CSP methods{,} suggesting it could be extended to even larger and more flexible molecules. On average{,} this optimisation improved the average reproduction of the eight experimental crystal structures (RMSD15 ) and experimental conformers (RMSD1) by 4% and 23%{,} respectively. The intermolecular interactions were then further optimised using distributed multipoles{,} derived from the molecular wave-function{,} to accurately describe the electrostatic component of the intermolecular energy. In all cases{,} the experimental crystal structures are close to the top of the lattice energy ranking. Phonon calculations on some of the lowest energy structures were also performed with DFTB3-D3 methods to calculate the vibrational component of the Helmholtz free energy{,} providing further insights into the solid-state behaviour of the target molecules. We conclude that DFTB3-D3 is a cost-effective method for optimising flexible molecules{,} bridging the gap between the approximate methods used in CSP searches for generating crystal structures and more accurate methods required in the final energy ranking.} }
Spin crossover and thermochemistry
As several properties can depend on the crystal packing, this also holds for the spin state of a material. Spin crossover compounds can be used as magnetic sensors and noncovalent interactions can influence their properties. I contributed to studies analyzing the relative stability of the high- and low-spin state of a few spin crossover complexes.
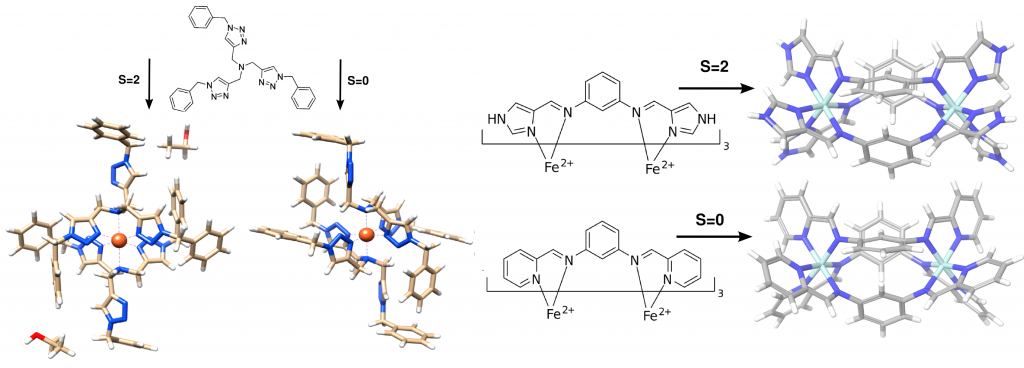
In collaboration with the group of Gerhard Erker, I analyzed the thermochemistry and some crystal packing effects in frustrated lewis pair (FLP) compounds. FLPs can activate small molecules like H2 and my theoretical studies helped interpreting thermodynamical features.
For more information, see for example:
- D. Schweinfurth, S. Demeshko, S. Hohloch, M. Steinmetz, J. G. Brandenburg, S. Dechert, F. Meyer, S. Grimme, and B. Sarkar, "Spin crossover in Fe(II) and Co(II) complexes with the same click-derived tripodal ligand," Inorg. Chem., vol. 53, p. 8203–8212, 2014. doi:10.1021/ic500264k
[BibTeX] [Abstract]
The complexes [Fe(tbta)2](BF4)2·2EtOH (1), [Fe(tbta)2](BF4)2·2CH3CN (2), [Fe(tbta) 2](BF4)2·2CHCl3 (3), and [Fe(tbta)2](BF4)2 (4) were synthesized from the respective metal salts and the click-derived tripodal ligand tris[(1-benzyl- 1H-1,2,3-triazol-4-yl)methyl]amine (tbta). Structural characterization of these complexes (at 100 or 133 K) revealed Fe-N bond lengths for the solvent containing compounds 1−3 that are typical of a high spin (HS) Fe(II) complex. In contrast, the solvent-free compound 4 show Fe−N bond lengths that are characteristic of a low spin (LS) Fe(II) state. The Fe center in all complexes is bound to two triazole and one amine N atom from each tbta ligand, with the third triazole arm remaining uncoordinated. The benzyl substituents of the uncoordinated triazole arms and the triazole rings engage in strong intermolecular and intramolecular noncovalent interactions. These interactions are missing in the solvent containing molecules 1, 2, and 3, where the solvent molecules occupy positions that hinder these noncovalent interactions. The solvent-free complex (4) displays spin crossover (SCO) with a spin transition temperature T1/2 near room temperature, as revealed by superconducting quantum interference device (SQUID) magnetometric and Moössbauer spectroscopic measurements. The complexes 1, 2, and 3 remain HS throughout the investigated temperature range. Different torsion angles at the metal centers, which are influenced by the noncovalent interactions, are likely responsible for the differences in the magnetic behavior of these complexes. The corresponding solvent-free Co(II) complex (6) is also LS at lower temperatures and displays SCO with a temperature T1/2 near room temperature. Theoretical calculations at molecular and periodic DFT-D3 levels for 1−4 qualitatively reproduce the experimental findings, and corroborate the importance of intermolecular and intramolecular noncovalent interactions for the magnetic properties of these complexes. The present work thus represents rare examples of SCO complexes where the use of identical ligand sets produces SCO in Fe(II) as well as Co(II) complexes.
@article{brandenburg_ref09, author = {D. Schweinfurth and S. Demeshko and S. Hohloch and M. Steinmetz and J. G. Brandenburg and S. Dechert and F. Meyer and S. Grimme and B. Sarkar}, title = {Spin crossover in {Fe(II)} and {Co(II)} complexes with the same click-derived tripodal ligand}, journal = {{Inorg. Chem.}}, year = {2014}, volume = {53}, pages = {8203--8212}, doi = {10.1021/ic500264k}, abstract = {The complexes [Fe(tbta)2](BF4)2·2EtOH (1), [Fe(tbta)2](BF4)2·2CH3CN (2), [Fe(tbta) 2](BF4)2·2CHCl3 (3), and [Fe(tbta)2](BF4)2 (4) were synthesized from the respective metal salts and the click-derived tripodal ligand tris[(1-benzyl- 1H-1,2,3-triazol-4-yl)methyl]amine (tbta). Structural characterization of these complexes (at 100 or 133 K) revealed Fe-N bond lengths for the solvent containing compounds 1−3 that are typical of a high spin (HS) Fe(II) complex. In contrast, the solvent-free compound 4 show Fe−N bond lengths that are characteristic of a low spin (LS) Fe(II) state. The Fe center in all complexes is bound to two triazole and one amine N atom from each tbta ligand, with the third triazole arm remaining uncoordinated. The benzyl substituents of the uncoordinated triazole arms and the triazole rings engage in strong intermolecular and intramolecular noncovalent interactions. These interactions are missing in the solvent containing molecules 1, 2, and 3, where the solvent molecules occupy positions that hinder these noncovalent interactions. The solvent-free complex (4) displays spin crossover (SCO) with a spin transition temperature T1/2 near room temperature, as revealed by superconducting quantum interference device (SQUID) magnetometric and Mo\"{o}ssbauer spectroscopic measurements. The complexes 1, 2, and 3 remain HS throughout the investigated temperature range. Different torsion angles at the metal centers, which are influenced by the noncovalent interactions, are likely responsible for the differences in the magnetic behavior of these complexes. The corresponding solvent-free Co(II) complex (6) is also LS at lower temperatures and displays SCO with a temperature T1/2 near room temperature. Theoretical calculations at molecular and periodic DFT-D3 levels for 1−4 qualitatively reproduce the experimental findings, and corroborate the importance of intermolecular and intramolecular noncovalent interactions for the magnetic properties of these complexes. The present work thus represents rare examples of SCO complexes where the use of identical ligand sets produces SCO in Fe(II) as well as Co(II) complexes.} }
- L. Wang, G. Kehr, C. G. Daniliuc, M. Brinkkötter, T. Wiegand, A. -L. Wübker, H. Eckert, L. Liu, J. G. Brandenburg, S. Grimme, and G. Erker, "Solid state frustrated lewis pair chemistry," Chem. Sci., vol. 9, pp. 4859-4865, 2018. doi:10.1039/c8sc01089g
[BibTeX] [Abstract] [Download PDF]
In solution the PCy$_3$/B(C$_6$F$_5$)$_3$ pair is rapidly deactivated by nucleophilic aromatic substitution. In the solid state deactivation is effectively suppressed and the active frustrated phosphane/borane Lewis pair splits dihydrogen or adds to sulfur dioxide. A variety of phosphane/B(C$_6$F$_5$)$_3$ pairs have been used to carry out active FLP reactions in the solid state. The reactions were analyzed by DFT calculations and by solid state NMR spectroscopy. The solid state dihydrogen splitting reaction was also carried out under near to ambient conditions with suspensions of the non-quenched phosphane/borane mixtures in the fluorous liquid perfluoromethylcyclohexane.
@Article{brandenburg_ref37, author ={L. Wang and G. Kehr and C. G. Daniliuc and M. Brinkk\"otter and T. Wiegand and A.-L. W\"ubker and H. Eckert and L. Liu and J. G. Brandenburg and S. Grimme and G. Erker}, title ={Solid state frustrated Lewis pair chemistry}, journal ={{Chem. Sci.}}, year ={2018}, volume = {9}, pages = {4859-4865}, year = {2018}, url = {../wp-content/papercite-data/pdf/brandenburg_ref37.pdf}, doi ={10.1039/c8sc01089g}, abstract ={In solution the PCy$_3$/B(C$_6$F$_5$)$_3$ pair is rapidly deactivated by nucleophilic aromatic substitution. In the solid state deactivation is effectively suppressed and the active frustrated phosphane/borane Lewis pair splits dihydrogen or adds to sulfur dioxide. A variety of phosphane/B(C$_6$F$_5$)$_3$ pairs have been used to carry out active FLP reactions in the solid state. The reactions were analyzed by DFT calculations and by solid state NMR spectroscopy. The solid state dihydrogen splitting reaction was also carried out under near to ambient conditions with suspensions of the non-quenched phosphane/borane mixtures in the fluorous liquid perfluoromethylcyclohexane.} }
- H. Buchholz, R. K. Hylton, J. G. Brandenburg, A. Seidel-Morgenstern, H. Lorenz, M. Stein, R. Hylton, and S. L. Price, "The thermochemistry of racemic and enantiopure molecular crystals for predicting enantiomer separation," Cryst. growth. des., vol. 8, pp. 4319-4324, 2017. doi:10.1021/acs.cgd.7b00582
[BibTeX] [Abstract] [Download PDF]
The separation of an enantiomer from a racemic mixture is of primary relevance to the pharmaceutical industry. The thermochemical properties of organic enantiopure and racemate crystals can be exploited to design an enantioselective crystallization process. The thermodynamic difference between the two crystal forms is accessible by two cycles which give the eutectic composition in solution. The 'sublimation cycle' requires calculating the lattice energy and phonon frequencies of the crystal structures. Experimental results from heat capacity and other thermodynamic measurements of enantiopure and racemic crystals are compared with a variety of molecular and crystal structure-based calculations. This is done for three prototypes of pharmaceutical-like molecules with different degrees of molecular flexibility. Differences in crystal packing result in varying temperature-dependent heat capacities and affect the sublimation thermodynamics, relative solubility and eutectic composition. Many simplifying assumptions about the thermodynamics and solubilities of the racemic and enantiopure crystals are critically evaluated. We show that calculations and experimental information using the sublimation cycle can guide the design of processes to resolve enantiomers by crystallization.
@article{brandenburg_ref27, title = {The thermochemistry of racemic and enantiopure molecular crystals for predicting enantiomer separation}, journal = {Cryst. Growth. Des.}, volume = {8}, pages = {4319-4324}, year = {2017}, doi = {10.1021/acs.cgd.7b00582}, url = {../wp-content/papercite-data/pdf/brandenburg_ref27.pdf}, author = {H. Buchholz and R. K. Hylton and J. G. Brandenburg and A. Seidel-Morgenstern and H. Lorenz and M. Stein and R. Hylton and S. L. Price,}, abstract={The separation of an enantiomer from a racemic mixture is of primary relevance to the pharmaceutical industry. The thermochemical properties of organic enantiopure and racemate crystals can be exploited to design an enantioselective crystallization process. The thermodynamic difference between the two crystal forms is accessible by two cycles which give the eutectic composition in solution. The 'sublimation cycle' requires calculating the lattice energy and phonon frequencies of the crystal structures. Experimental results from heat capacity and other thermodynamic measurements of enantiopure and racemic crystals are compared with a variety of molecular and crystal structure-based calculations. This is done for three prototypes of pharmaceutical-like molecules with different degrees of molecular flexibility. Differences in crystal packing result in varying temperature-dependent heat capacities and affect the sublimation thermodynamics, relative solubility and eutectic composition. Many simplifying assumptions about the thermodynamics and solubilities of the racemic and enantiopure crystals are critically evaluated. We show that calculations and experimental information using the sublimation cycle can guide the design of processes to resolve enantiomers by crystallization.} }
- J. G. Brandenburg, J. Potticary, H. A. Sparkes, S. L. Price, and S. R. Hall, "Thermal expansion of carbamazepine: systematic crystallographic measurements challenge quantum chemical calculations," J. Phys. Chem. Lett., vol. 8, pp. 4319-4324, 2017. doi:10.1021/acs.jpclett.7b01944
[BibTeX] [Abstract] [Download PDF]
We report systematic temperature-dependent X-ray measurements on the most stable carbamazepine polymorph. This active pharmaceutical ingredient is used to demonstrate how the thermal expansion can probe certain intermolecular interactions resulting in anisotropic expansion behavior. We show that most structural features can be captured by electronic structure calculations at the quasi-harmonic approximation (QHA) provided a dispersion-corrected density functional based method is employed. The impact of thermal expansion on the phonon modes and hence free energy contributions is large enough to impact the relative stability of different polymorphs.
@article{brandenburg_ref30, author = {J. G. Brandenburg and J. Potticary and H. A. Sparkes and S. L. Price and S. R. Hall}, title = {Thermal expansion of carbamazepine: Systematic crystallographic measurements challenge quantum chemical calculations}, journal = {{J. Phys. Chem. Lett.}}, volume = {8}, pages = {4319-4324}, year = {2017}, doi = {10.1021/acs.jpclett.7b01944}, url = {../wp-content/papercite-data/pdf/brandenburg_ref30.pdf}, abstract={We report systematic temperature-dependent X-ray measurements on the most stable carbamazepine polymorph. This active pharmaceutical ingredient is used to demonstrate how the thermal expansion can probe certain intermolecular interactions resulting in anisotropic expansion behavior. We show that most structural features can be captured by electronic structure calculations at the quasi-harmonic approximation (QHA) provided a dispersion-corrected density functional based method is employed. The impact of thermal expansion on the phonon modes and hence free energy contributions is large enough to impact the relative stability of different polymorphs.} }